1. INTRODUCCIÓN
El coronavirus (COVID-19) es una enfermedad infecciosa causada por el virus del SARS-CoV-2 que ha generado una crisis sanitaria a nivel mundial. El 11 de marzo del 2020 dicha enfermedad fue catalogada como pandemia, una de las regiones más afectadas fue Latino América y el Caribe, debido a varios factores como densidad poblacional, incapacidad en los sistemas sanitarios, entre otras. En el presente estudio se realizará un análisis general de los datos de contagios y muertes de diez países de América Latina con la finalidad de identificar qué país ha manejado mejor la pandemia según sus resultados. Se realizo una predicción con variables con el número de contagios y muertes causadas por la Covid-19, utilizando los datos obtenidos en la página oficial de la OMS (Organización mundial de la salud) (OMS, 2019) para generar un análisis estadístico en el software RStudio.
Para este estudio útil se utilizará el modelo ARIMA (Newbold,1983) y el método Biplot (Gabriel, 1980), los cuales son útiles para representar una gráfica de datos multivariantes. El Biplot tiene como objetivo la aproximación de una matriz de datos, de tal forma que permita su descripción o modelización, es una representación gráfica por medio de planos factoriales que reflejan las características más importantes de la matriz de datos analizada en una dimensión reducida. (Cárdenas et al., 2007)
El modelo ARIMA (AutoRegresive Integrated Moving Average), permite realizar una descripción de un valor estudiado como una determinada función lineal de los datos originales del análisis, además, esta función puede incluir análisis de los componentes cíclico o estacional de la serie temporal. Es decir, debe contener la serie descrita los elementos necesarios para describir originalmente el fenómeno. (González, 2009).
Se han realizado varios estudios por separados de las técnicas a utilizar, tales como análisis mediante modelo ARIMA de COVID-19 (Araujo, 2022), predicción del fondo monetario (Fan, 2022), entre otros, así también estudios donde se ha representado mediante un biplot dinámico, tales como, análisis de índices de sostenibilidad (De la Hoz, 2022), análisis de evolución de rankings de universidades en diferentes años (Gomez-Marcos, 2021).
El propósito de este estudio es demostrar gráficamente los efectos que ha tenido la pandemia haciendo una correlación entre el número de contagios y muertes causadas por la Covid-19, y el número de habitantes, mensualmente en los principales países de América del Sur, y luego hacer un modelo predictivo que permita pronosticar los contagios y muertes para septiembre y octubre y así conocer la tasa de letalidad.
2. MATERIALES Y MÉTODOS
Los modelos ARIMA descrito por Box y Jenkins, nace de que la mayoría de las series no son estacionarias, dificultando poder trabajar con este tipo de serie temporal no estacionaria (Box & Jenkins, 1970), donde se expresa que una serie es estacionaria cuando su varianza, covarianza y su media no varían en un determinado tiempo.
La mayoría de las series temporales analizadas en la econometría no son estacionarias, pero mediante el proceso de diferenciación de un número definido de veces a la serie de partida se obtiene una serie estacionaria, pudiendo así aplicar la metodología ARIMA a la serie diferenciada.
Generalmente, una serie de tiempo del tipo ![]() Ec. (1) admite una representación de la serie autorregresiva
integrada y de promedios móviles, en el orden p (procesos autorregresivos), d
(diferencias hasta que sea estacionario) y q (orden del proceso de medias
móviles) respectivamente, y se denota por ARIMA (p, d, q).
Ec. (1) admite una representación de la serie autorregresiva
integrada y de promedios móviles, en el orden p (procesos autorregresivos), d
(diferencias hasta que sea estacionario) y q (orden del proceso de medias
móviles) respectivamente, y se denota por ARIMA (p, d, q).
![]() (1)
(1)
Donde p denota el número de términos autorregresivos de la serie, del número de veces que la serie es diferenciada hasta lograr que la misma sea estacionaria y q el orden del proceso de la media móvil invertible de la serie.
Para denotar estos modelos se pueden distinguir cuatro etapas, las cuales se llevan de una manera iterativa mediante el proceso que se describe a continuación:
· Identificación: Se ordena los datos cronológicamente donde se buscará sugerir un modelo que viablemente pueda ser analizado. El objeto es poder describir cuáles son los valores que permitan reproducir la serie temporal apropiadamente.
· Diferenciación de la serie de tiempo. Durante este proceso se examina la estacionariedad de la serie, mediante los diagramas de autocorrelación, usando los términos ACF el cual calcula la función de autocorrelación simple de una serie de tiempo, y PACF el cual se expresa como la función de autocorrelación parcial, y elección del orden del modelo.
· Ajuste del modelo de la Serie Temporal ARIMA. Esto nos permite obtener los coeficientes de determinación.
· Predicción. Seleccionado el mejor modelo obtenido de los pasos anteriores, se pueden generar pronósticos en términos probabilísticos de los valores futuros de la serie original de datos. (Massó Ibarra, 2018)
Por otro lado, las representaciones Biplot (Gabriel, 1980) son representaciones graficas en planos factoriales que en una dimensión de representación reducida permiten reflejar las características más importantes de la matriz de datos original, generando una calidad de representación reducida de los datos originales. La principal diferencia respecto a otras técnicas de representación es que en este caso se logra representan en conjunto las variables expresadas en las columnas y a los individuos de estudio, representados en las filas; es decir, en el mismo gráfico vectorial aparecen superpuestos los puntos o vectores fila y puntos o vectores columna de la matriz de datos original. Las nuevas investigaciones utilizan el Biplot como método gráfico para representar en baja dimensión los resultados de matrices de datos extensas o con varias variables con una alta representación de los datos.
Un Biplot genera la mejor aproximación de los datos en dimensión reducida (generalmente dos dimensiones, que recogen la máxima representación) de la distribución de una matriz de datos multivariante. Representa de una manera superpuesta sobre dicha representación, puntos o vectores en forma de flechas que expresan las variables analizadas (columnas); e indican la posición y dirección por medio de la longitud del vector y la relación en la que mejor se muestra el cambio individual de cada una de las variables y su relación en conjunto entre estas. El prefijo “bi” indica la superposición en el mismo espacio vectorial de los marcadores individuos (filas) y variables (columnas) de la matriz de datos. Dichos marcadores o puntos se representan en un espacio vectorial cuya dimensión va a ser menor que la representada en la matriz original de datos. Para la interpretación de la representación Biplot se consideran conceptos geométricos fácil de interpretar, así, por ejemplo:
· La relación que se da entre individuos (filas) es una función inversa de la distancia entre cada individuo.
· Las longitudes y los ángulos que se generan por cada flecha o vector, representando cada una de las variables que se interpretan en términos de un análisis de variabilidad y covariabilidad respectivamente entre las columnas.
· La relación entre las columnas y las filas se leen en términos del producto escalar, es decir, en términos de las proyecciones que se dan en el espacio vectorial de los puntos o marcadores “fila” sobre las flechas o vectores “columna”, en el gráfico.
Los Biplot más importantes descritos por Gabriel (1980) son los conocidos como el GH-Biplot y JK-Biplot (Galindo,1980). El GH-Biplot descrito genera una mejor calidad en la representación por medio de vectores de las columnas (variables) que para las filas (individuos); por otra parte, el JK-Biplot consiguen una mayor calidad de representación para los marcadores filas, que para los marcadores columnas. (Nualles, 2002). El biplot dinámico (Egido, 2015), basado en el HJ-Biplot (Galindo, 1986) realiza un análisis multivariable tomando en consideración un punto de partida considerado como la línea de base la cual se considera proporciona la mejor información entre individuos y variables y las relaciona entre ellos.
Otra de las librerías que se han usado es Highcharter (Kunst, 2020), la cual forma parte de los paquetes más importantes de RStudio. La importancia del uso de esta librería consta en que se pueden hacer gráficos dinámicos de Highcharts. Considerando lo antes mencionado, se puede indicar que Highcharts es una librería escrita en lenguaje R que interactúa con gráficos JavaScript flexible, la cual tiene muchas características esenciales para el análisis, se ha tomado en cuenta las siguientes:
· Permite realizar distintos tipos de gráficas, sin variar el estilo de cada una, las gráficas a utilizar son: dispersión, burbuja, línea, serie de tiempo, mapas de calor, treemap, gráficos de barras, redes, etc.
· También permite realizar distintos objetos en R con una sola función, como la función hchart, con la cual se puede generar a partir de data.frames varios tipos de histogramas, también posee otras funcionabilidades descritas en varias funciones como: ts, mts, xts, stl, ohlc, acf, pronósticos, mforecast, ets, igraph, dist, dendrogram, phylo, survfit clases.
La finalidad de aplicar Highcharts es para poder realizar mapas dinámicos, lo cual es necesario para nuestro análisis. La función hcmap, que forma parte de la librería Highcharter, es la indicada para poder ejecutar lo requerido, ya que nos permite crear mapas dinámicos de manera rápida y sencilla, lo único que se debe hacer es elegir un mapa desde una (url) de la colección highmaps y usarlo con nuestros datos y personalización deseada como se mostrará más adelante. Esta función se encarga de descargar el mapa ya listo desde la (url) elegida, posterior a ello genera el gráfico rápidamente.
Con la finalidad de agregarle datos a la gráfica usamos varios dataframe que contengan cada una de las variables identificadoras (países, números de contagiados, números de fallecidos y tasa de letalidad) y la variable cuantitativa deseada, para evitar errores e ingresar manualmente los nombres de los países usamos la función get_data_from_map.
Para agregar más detalles y personalizable se usaron los siguientes argumentos borderColor, borderWidth, tooltip, hc_title, hc_subtitle, hc_tooltip, hc_add_series_map, hc_coloraxis, hc_legend, hc_mapNavigation, hc_add_theme, hc_add_annotation y hc_chart que son funciones propias de highcharter. (Regenstein, 2018)
El índice de letalidad, que nos muestra el número de muertes generados en un lapso específico de tiempo producto de una causa especifica, sin contar a toda la población, sino solamente a la población afectada (Figueiredo et al., 2022), el cual se ha calculado para el presente estudio de acuerdo con los datos observados.
3. RESULTADOS Y DISCUSIÓN
Se puede observar en la Figura 1 que Ecuador es el país con mayor taza de letalidad en América del Sur con un 5.87%, seguido de Perú con una tasa del 4.63% y Bolivia con 4.16% según los casos reportados a la OMS hasta agosto 2020. Con esta diferencia de resultados entre Ecuador, Perú y Bolivia se puede inferir que existe una desigualdad en la capacidad de los sistemas de salud para enfrentar la pandemia.
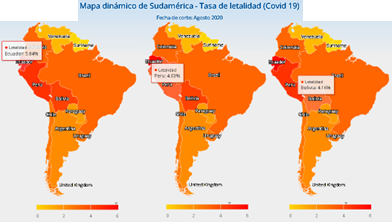
Figura 1. Mapa dinámico de Sudamérica-tasa de letalidad por Covid-19
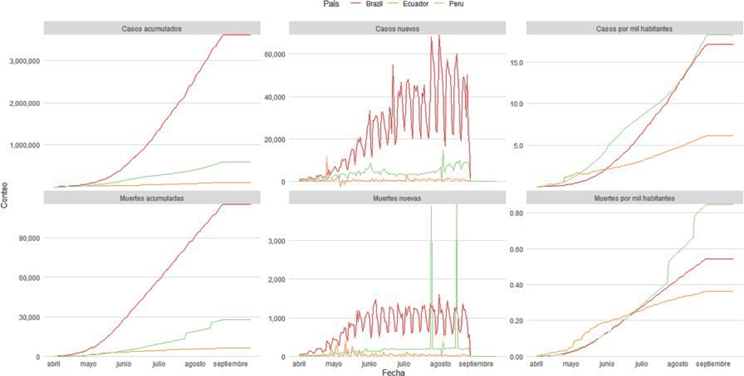
Figura 2. Gráfico combinado de casos y muerte con COVID-19. Brasil, Perú y Ecuador
En la Figura 2 se puede observar que en Perú se tendría por cada mil habitante aproximadamente 20 personas contagiadas y una persona fallecida por SARS- CoV2. En Brasil se tendría por cada mil habitantes aproximadamente 18 personas contagiadas y de acuerdo con la gráfica se estimaría que por cada dos mil habitantes se tendría una persona fallecida por COVID-19. En Ecuador se tendría por cada mil habitantes aproximadamente siete personas contagiadas y de acuerdo con la gráfica se estimaría que por cada tres mil habitantes se tendría una persona fallecida por coronavirus.
En la Figura 3, de acuerdo con el análisis realizado Ecuador en el mes de agosto, tiene una media menor con relación a los demás países, y su nivel de muertes y contagios se ha podido reducir en el mes de agosto. En cuanto a Perú y Chile en el mes de abril si se coloca una perpendicular a nivel de muertos se observaría que aumentaron, pero a nivel de contagio, disminuyeron.
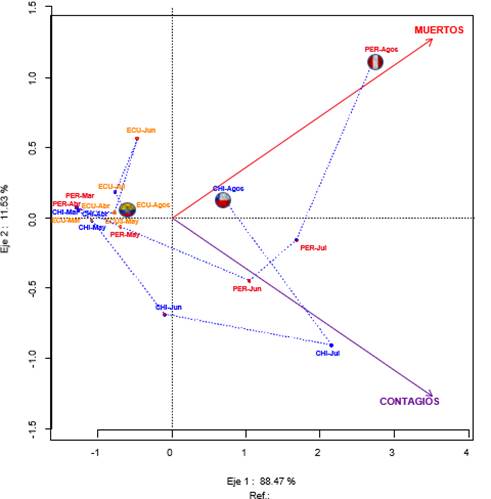
Figura 3. Biplot dinámico de muertes y contagios en Ecuador, Perú y Chile
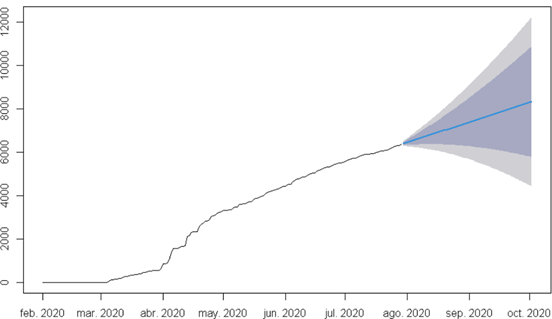
Figura 4. Gráfica ARIMA de fallecidos en el Ecuador sep.-oct.
La Figura 4 muestra la predicción de los fallecidos que tendría Ecuador a finales de octubre, la línea azul indica la tendencia que tiene los datos a aumentar la cantidad de fallecidos, en donde la zona más oscura del grafico indica los límite superiores e inferiores de los datos, con un nivel de confianza del 80% y la zona más clara indica los limites superiores e inferiores de los datos con un nivel de confianza del 95%. Como resultado se obtuvo que el mes de octubre se esperaría una media de 8326 personas fallecidas con un nivel de confianza del 95% teniendo un máximo de 12212 y un mínimo de 4440 personas contagiadas.
En la Tabla 1 se puede observar que la tasa de letalidad que tendrá Ecuador en el mes de septiembre es de 5,49% y en el mes de octubre 5,10%, estos valores fueron calculados a partir de los datos generados en la predicción realizada por el modelado ARIMA, evidenciando que el porcentaje de letalidad en Ecuador ha disminuido en comparación con la tasa obtenida en el mes de agosto de 5,87%.
Tabla 1. Tasa de letalidad en Ecuador en el mes de septiembre y octubre
|
|
Contagios en Ecuador |
Muertes en Ecuador |
Tasa de Letalidad |
|
01/09/2020 |
113562.4 |
6518.6 |
5.49% |
|
12/09/2020 |
114468.8 |
6548.8 |
|
|
… |
… |
… |
|
|
29/09/2020 |
138943.6 |
7362.2 |
|
|
30/09/2020 |
139850.0 |
7392.4 |
|
|
01/10/2020 |
140465.5 |
7422.5 |
5.10% |
|
02/10/2020 |
141663.0 |
7452.6 |
|
|
… |
… |
… |
|
|
30/10/2020 |
167044.2 |
8296.6 |
|
|
31/10/2020 |
167950.6 |
8326.4 |
CONCLUSIONES
De acuerdo con el estudio de modelo de predicción para el número contagios y fallecidos en Ecuador, se pudo evidenciar que para el mes de octubre se tendrá una media de 167951 personas contagiadas con un nivel de confianza del 95% con un máximo de 211542 y un mínimo de 124359 de personas contagiadas por Covid-19. Con el Biplot dinámico se determinó que Ecuador en subconjunto siempre ha mantenido un nivel de contagio y letalidad menor que Perú y Chile, debido a diferentes factores como políticas de salud universales que garanticen el derecho a la vida. Además, los resultados obtenidos mediante de la gráfica combinada se puede describir la correlación entre los contagios y muertes, y la cantidad de habitantes. De los análisis realizados sobre la tasa de letalidad de cada país mostrados en la figura 1, se puede decir en términos generales que Ecuador es el país más afectado a lo largo de esta pandemia con una mayor taza de letalidad en América del Sur. Por otra parte, la predicción realizada ha permitido conocer la tendencia que tiene los datos a aumentar tanto el número de fallecidos como de contagiados en contraste se obtiene una tasa de letalidad a la baja en Ecuador, con una predicción de 5,10% en el mes de octubre.
Declaración de conflictos
Los autores declararon que no existe ningún conflicto de interés potencial dentro de esta investigación, autoría y/o publicación de este artículo.
REFERENCIAS
Araújo Morais, L. R., & da Silva Gomes, G. S. (2022). Forecasting daily Covid-19 cases in the world with a hybrid ARIMA and neural network model. Applied Soft Computing, 126. https://doi.org/10.1016/j.asoc.2022.109315
Box, G. E., Jenkins, G. M. (1970). Time Series Analysis: Forecasting and Control, Holden-Da: San Francisco.
Cárdenas, O., Vicente Villardon, J. L., & Galindo Villardón, M. P. (2007). Los Métodos Biplot: Evolución y Aplicaciones. Revista Venezolana De Análisis De Coyuntura, XIII (1), 279-303. https://www.redalyc.org/pdf/364/36413113.pdf
Egido, J., Galindo, P. (2015). Dynamic Biplot. Evolution of the Economic Freedom in The European Union. British Journal of Applied Science and Technology, 11(3), 1-13. https://DOI:10.9734/BJAST/2015/20289
Fan, W. (2022). Prediction of Monetary Fund Based on ARIMA Model. Procedia Computer Science, 208, 277-285. https://doi.org/10.1016/j.procs.2022.10.040
Figueiredo, A. M. D., Daponte, A., Figueiredo, D. C. M. M. D., Gil-García, E., & Kalache, A. (2022). Letalidad De La COVID-19: Ausencia De Patrón Epidemiológico. Gaceta Sanitaria, 35, 355-357. doi: 10.1016/j.gaceta.2020.04.001
Gabriel, K. R. (1980). Biplot Display Of Multivariate Matrices For Inspection Of Data And Diagnosis. Rochester Univ Ny.
Galindo, M. P. (1986). Una Alternativa De Representación Simultánea. Hj-Biplot. Qüestiió: Quaderns D'estadística I Investigació Operativa, 10(1), 13-23. https://dialnet.unirioja.es/servlet/articulo?codigo=2360880
González Casimiro, M. P. (2009). Análisis De Series Temporales: Modelos Arima. Economía Aplicada Iii/Ekonomia Aplikatua Iii, Upv/Ehu. https://Doi.Org/10/12492
Gómez-Marcos, M.-T., Ruiz-Toledo, M., Vicente-Galindo, M.-P., Martín-Rodero, H., Ruff-Escobar, C., & Galindo-Villardón, M.P. (2021). Multivariate dynamics of Spanish universities in international rankings. Profesional De La información, 30(2). https://doi.org/10.3145/epi.2021.mar.10
Kunst, J. (2020). Highcharter: A Wrapper For The 'Highcharts' Library. Tomado De Https://Jkunst.Com/Highcharter/Authors.Html
Massó Ibarra, V. (2018). Rpubs—Modelos Arima. Recuperado 17 De Octubre De 2022, De https://Rpubs.Com/Valeamasso/386527
Newbold, P. (1983). Arima Model Building And The Time Series Analysis Approach To Forecasting. Journal Of Forecasting, 2(1), 23-35. https://Doi.Org/10.1002/For.3980020104
Nualles, M. V. (2002). Los Métodos Biplot Como Herramienta De Análisis De Interacción De Orden Superior En Un Modelo Lineal/Bilineal. [Disertación de Licenciatura, Universidad de Salamanca. España] http://repositorio.geotech.cu/jspui/handle/1234/2816
OMS. (2019). Nuevo Coronavirus 2019. OMS. Recuperado 17 De Octubre De 2022, De https://Www.Who.Int/Es/Emergencies/Diseases/Novel-Coronavirus-2019
Regenstein, J. K., & Jr. (2018). Finanzas Reproducibles Con R: Flujos De Código Y Aplicaciones Brillantes Para Análisis De Cartera. Chapman and Hall/CRC: New York. https://doi.org/10.1201/9781351052627